Network flows are a subclass of optimisation problems which (as you might have guessed) model flows on networks. We formulate these problems using terminology and notation from graph theory. Consider a directed graph, consisting of a set of nodes and arcs (see Figure 1). Now imagine you would like to send an amount of 'flow' down some of the arcs, usually representing some commodity, such as water through pipes or electricity through cables. We associate with each arc a cost per unit flow, this could represent time, distance or financial cost for example. Furthermore, we assume that each arc has a upper and lower bound on the amount of flow which can be sent, the lower bound is usually assumed to be zero and the upper bound viewed to represent the capacity of that arc.
Examples of this type of problem include the movement of cargo through railway networks or water and oil through pipes (not mixed together). They have a wide range of formulations applicable to many different contexts, for example shortest paths and travelling salesman problems can be formulated as network flow problems. For a introduction to a couple of network flow problems take a look at my previous post.
L. R. Ford Jr and D. R. Fulkerson are largely credited with laying foundations for the study of network flows with their book Flows Through Networks (1962) [2]. They formulated the maximum flow problem, citing inspiration to a secret report [3] written for the US Air Force by T. E. Harris in conjunction with General G. S. Ross in 1955. This report was declassified by the Pentagon in 1999 at the request of Schrijver.
When formulating the maximum flow problem in [2], Ford and Fulkerson made reference to Harris and Ross, claiming they "had formulated a simplified model of railway traffic flow, and pinpointed this particular problem as the central one suggested by the model". However, Schrijver claims that Harris and Ross were not actually interested in finding the maximum flow but instead the so-called minimum cut.
As I mentioned earlier, each of these arcs has an upper bound on the flow, referred to as its capacity. These are the main constraints in the maximum flow problem, since if there were none we could technically send an infinite amount of flow, so there would be no problem to solve. Now, given a directed cut, sum the capacities of all arcs and call this the cut capacity.
One can now ask the following question: out of all possible directed cuts of the network, which one has the lowest capacity? We call the directed cut that answers this question the minimum cut. According to Schrijver it was this, not the maximum flow, that Harris and Ross were intending to find. These may or may not seem to you like two completely different problems, however, a theorem due to Ford and Fulkerson states that they are actually one and the same. This is know as the Max-flow Min-cut Theorem, and it says that the maximum amount of flow that can be sent through a network from source to sink is equal to the minimum cut.
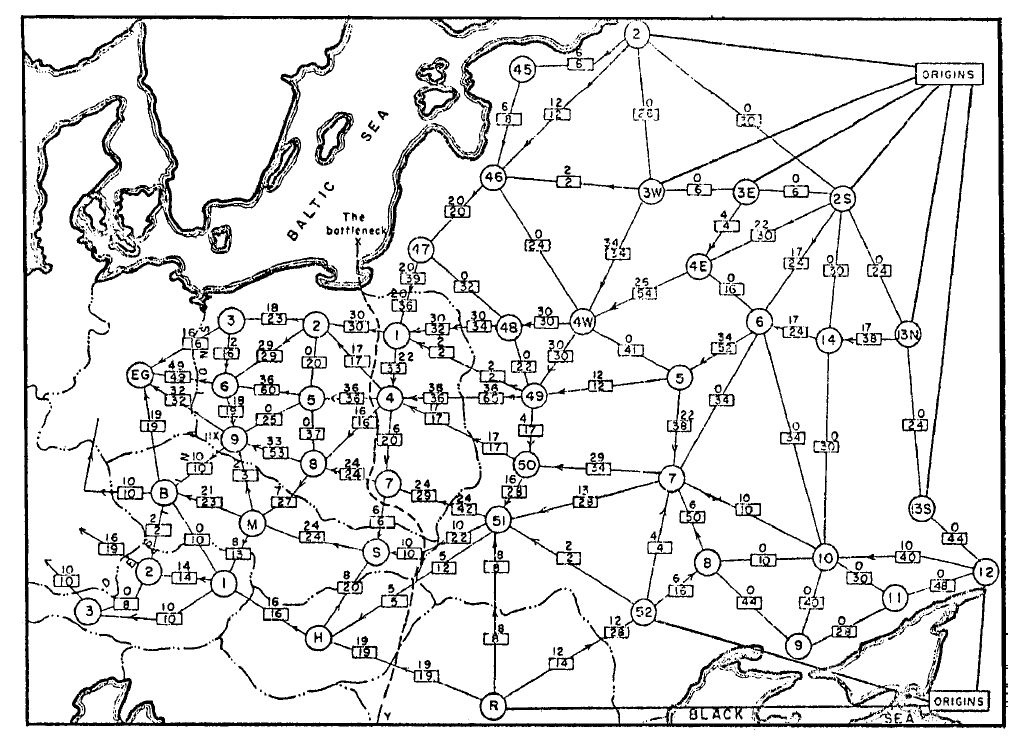
A diagram of the network can be seen in Figure 2 below. To cause most disruption via interdiction they proposed finding the so called 'bottleneck' (see diagram) where a reduction in arc flow capacity would have most impact on the maximum flow that could be sent through the network. However, this is nothing more than the minimum cut! Since if you decrease the capacity on any arc in the minimum cut this will reduce the maximum flow of the network.
Examples of this type of problem include the movement of cargo through railway networks or water and oil through pipes (not mixed together). They have a wide range of formulations applicable to many different contexts, for example shortest paths and travelling salesman problems can be formulated as network flow problems. For a introduction to a couple of network flow problems take a look at my previous post.
The maximum flow problem
One of the simplest network flow problems is the maximum flow problem, discussed in my previous post. This concerns finding the maximum amount of 'flow' that can be sent from one point in the network to another. A brilliant insight into the origins of this problem is given by Schrijver [1].L. R. Ford Jr and D. R. Fulkerson are largely credited with laying foundations for the study of network flows with their book Flows Through Networks (1962) [2]. They formulated the maximum flow problem, citing inspiration to a secret report [3] written for the US Air Force by T. E. Harris in conjunction with General G. S. Ross in 1955. This report was declassified by the Pentagon in 1999 at the request of Schrijver.
When formulating the maximum flow problem in [2], Ford and Fulkerson made reference to Harris and Ross, claiming they "had formulated a simplified model of railway traffic flow, and pinpointed this particular problem as the central one suggested by the model". However, Schrijver claims that Harris and Ross were not actually interested in finding the maximum flow but instead the so-called minimum cut.
Maximum flow vs minimum cut
A cut is essentially a subset of the arcs in a network, induced by some partitioning of the nodes. Consider a network with a source node \(s\) , where we would like to send the flow from, and a sink node \(t\) where we would like it to go (Figure 1). Take some subset of the nodes that includes the source, for example the nodes within the green ellipse, and consider the arcs leaving this set (we have 6 such arcs in this case). We call this collection of arcs the cut, or more correctly the directed cut.
| Figure 1 - Example of a network |
As I mentioned earlier, each of these arcs has an upper bound on the flow, referred to as its capacity. These are the main constraints in the maximum flow problem, since if there were none we could technically send an infinite amount of flow, so there would be no problem to solve. Now, given a directed cut, sum the capacities of all arcs and call this the cut capacity.
One can now ask the following question: out of all possible directed cuts of the network, which one has the lowest capacity? We call the directed cut that answers this question the minimum cut. According to Schrijver it was this, not the maximum flow, that Harris and Ross were intending to find. These may or may not seem to you like two completely different problems, however, a theorem due to Ford and Fulkerson states that they are actually one and the same. This is know as the Max-flow Min-cut Theorem, and it says that the maximum amount of flow that can be sent through a network from source to sink is equal to the minimum cut.
Why were Harris and Ross interested in minimum cut?
Back in 1955 the tensions between the US and the Soviet Union were very high, with both sides working hard to gain a military advantage over their counterpart. In the midst of this, Harris and Ross were given the challenge of studying the Soviet railway network, to find the most effective way of interdicting it, i.e. damaging it via means such as air power to prevent the movement of goods such a soldiers and weaponry.A diagram of the network can be seen in Figure 2 below. To cause most disruption via interdiction they proposed finding the so called 'bottleneck' (see diagram) where a reduction in arc flow capacity would have most impact on the maximum flow that could be sent through the network. However, this is nothing more than the minimum cut! Since if you decrease the capacity on any arc in the minimum cut this will reduce the maximum flow of the network.
Parting remarks
This glimpse into the origins of the maximum flow problem gives an insight into the problems that operational researchers were trying to tackle in the early days. Today, however, this and other network flow problems have much more beneficial uses such as modelling traffic on roads, electricity through wires or data through telecommunications networks, improving their performance and reducing their costs.
References
[1] Schrijver, A. Math. Program. (2002) 91: 437. https://doi.org/10.1007/s101070100259
[2] Ford, L.R., Jr, Fulkerson, D.R. (1962): Flows in Networks. Princeton University Press, Princeton, New Jersey
[3] Harris, T.E., Ross, F.S. (1955): Fundamentals of a Method for Evaluating Rail Net Capacities. Research Memorandum RM-1573, The RAND Corporation, Santa Monica, California
[2] Ford, L.R., Jr, Fulkerson, D.R. (1962): Flows in Networks. Princeton University Press, Princeton, New Jersey
[3] Harris, T.E., Ross, F.S. (1955): Fundamentals of a Method for Evaluating Rail Net Capacities. Research Memorandum RM-1573, The RAND Corporation, Santa Monica, California



Nice post, I love military applications of OR.
ReplyDelete